Mi az mágneses momentum?
Miért válnak egyes anyagok mágnesekké, míg mások nem? A válasz egy mágneses momentum nevű tulajdonságban rejlik.
A mágneses momentum egy vektormennyiség, amely kifejezi egy mágneses forrás, például egy atom vagy egy mágnes erősségét és irányát.
Ez egy alapvető fogalom mind klasszikus, mind kvantum mágnesességben, és mindent alakít, az MRI gépektől a mágneses érzékelőkig.
Mi a mágneses momentum egy hurknál?
Mi történik, amikor áram folyik egy kör alakú vezetékben? Az lesz egy apró mágnes.
A hurk mágneses momentumát az áram és a hurok területe szorzataként határozzuk meg, amely merőleges a hurok síkjára.
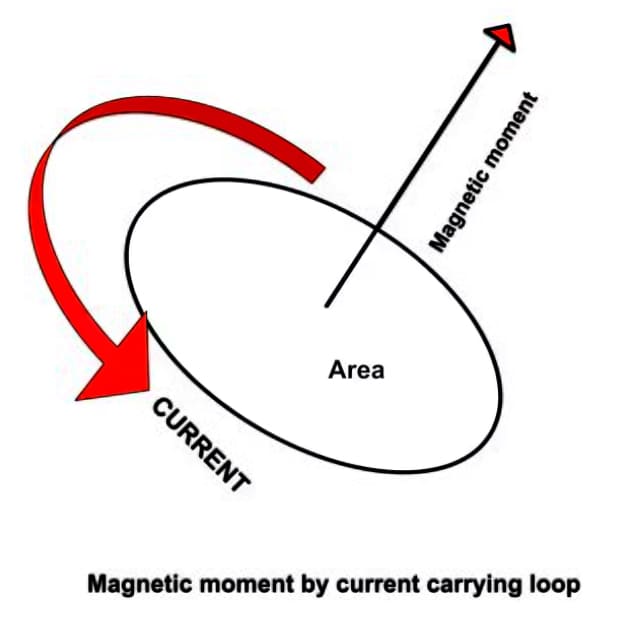
mágneses momentum áramot vezető hurallal
Miért viselkedik egy hurok mint egy mágnes
Egy áramot vezető hurok mágneses mezőt generál. Ez a mágneses mező iránnyal rendelkezik — a jobb kéz szabálya szerint — és erősséggel. A hurok mágneses momentumát (( \vec{m} )) a következőképpen adjuk meg:
[\vec{m} = I \cdot A \cdot \hat{n}]
Ahol:
- ( I ) az áram
- ( A ) a hurok területe
- ( \hat{n} ) a síkra merőleges egységvektor
| Tényező | Hatás a mágneses momentumra |
|---|---|
| Nagyobb terület | Növeli a mágneses momentumot |
| Magasabb áram | Növeli a mágneses momentumot |
| Több hurok | Fokozza az összmomentumot |
Segítettem mérnököknek a mágneses momentum kiszámításában egyedi tekercsekhez. Egy érzékelő ügyfél projektjében a hurkok számának növelése lehetővé tette, hogy gyengébb mágneses mezőket észleljenek nagyobb pontossággal.
Mi a mágneses momentum szabálya?
Van-e mód a mágneses momentum irányának előrejelzésére? Igen, egyszerű.
A jobb kéz szabályát használjuk a mágneses momentum irányának meghatározására: tekerje az ujjait az áram irányába, és a hüvelykujj a momentum irányába mutat.

jobb kéz szabálya a mágneses momentumhoz–fotó innen elektromágnesesség
A szabály alkalmazása valódi rendszerekben
Egy tekercs vagy hurk esetében a mágneses momentum vektor iránya a jobb kéz szabályát követi. Ez segít:
- Mágneses mező érzékelők tervezése
- A forgatónyomaték megértése egy tekercsen egy mágneses mezőben
- N/S pólusok meghatározása mágnesesen töltött szerkezetekben
Így alkalmazható a szabály a gyakori felállásokra:
| Felállás | Mágneses Momentum Irány |
|---|---|
| Vízszintes óramutató járásával megegyező hurk | Az oldal felé |
| Vízszintes ellentétes óramutató járásával megegyező hurk | Az oldal felől kifelé |
| Függőleges tekercs | Felfelé vagy lefelé az áram szerint |
Amikor mágneses szerkezeteket tervezek, mindig vázlatosan felrajzolom a tekercs elhelyezkedését, és a jobbkéz szabályt használom. Ez időt takarít meg, elkerüli a hibákat, és biztosítja, hogy a mező összhangban legyen a tervezési céllal.
Hogyan számíthatjuk ki a mágneses momentumot?
Nem kell találgatni a mágneses momentumot – ki tudod számítani.
A mágneses momentumot a következő képlet segítségével számítjuk ki: ( m = N \cdot I \cdot A ), ahol N a tekercs fordulatszáma, I az áram, és A minden egyes forduló területe.
Példák és alkalmazások
Részletesen bontsuk ki a képletet:
[m = NIA]
- ( N ): A tekercs fordulatszáma
- ( I ): Az áram a tekercsen keresztül
- ( A ): Minden egyes forduló által bezárt terület (m²-ben)
Példa:
Ha egy tekercsnek 100 fordulata van, 0,5 A áramot hordoz, és minden forduló területe 0,01 m²:
[m = 100 \cdot 0.5 \cdot 0.01 = 0.5 \text{ A·m}^2]
Gyakorlati felhasználások:
- Áramkörökben lévő forgatónyomaték számítása elektromos motorokban
- A mágneses érzékelők mezőerősségének becslése
- Induktorok és transzformátorok tervezése
| Parameter | Egység | Jellemző tartomány |
|---|---|---|
| ( I ): | Amper | 0,01 – 10 A |
| ( A ) | Négyzetméter | 0,0001 – 0,1 m² |
| ( m ) | A·m² | 0,001 – 10 A·m² |
Az ügyfelek gyakran kérdezik, hogyan lehet növelni a mágneses hatást az áram növelése nélkül. A válasz általában: növelje a hurkolás területét vagy a fordulatszámok számát.
Következtetés
A mágneses momentum kulcsfontosságú tulajdonság a mágneses rendszerek megértéséhez. Megmutatja, milyen erős és milyen irányban hat egy mágnes, legyen az egy apró elektron vagy egy nagy generátorkábel.




[…] Ezek a sokféle alkalmazások hangsúlyozzák, miért elengedhetetlen a mágneses anyagok folyamatos innovációja a magas teljesítmény és fenntarthatóság iránti igények kielégítése érdekében ma Magyarországon. A mélyebb megértés érdekében tekintse meg Mi az a Mágneses Momentum.