磁気モーメントとは?
なぜ磁石になる物質とそうでない物質があるのでしょうか?その答えは、磁気モーメントと呼ばれる特性にあります。
磁気モーメントは、原子や磁石のような磁気源の強さと方向を表すベクトル量です。 磁石。
これは、古典磁気学と量子磁気学の両方における基礎的な概念であり、MRI装置から磁気センサーまで、あらゆるものを形作っています。
ループの磁気モーメントとは?
円形の導線に電流が流れるとどうなるでしょうか?それは小さな磁石になります。
ループの磁気モーメントは、電流とループの面積の積として定義され、ループの面に垂直な方向を向いています。
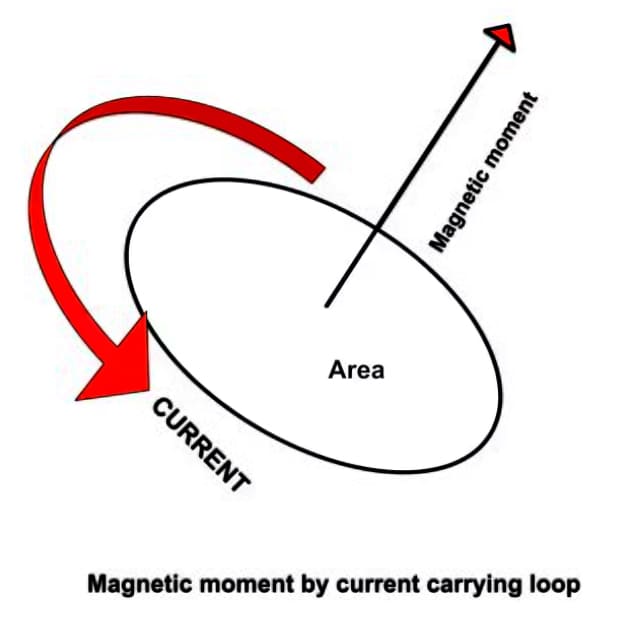
電流を流すループによる磁気モーメント
ループが磁石のように振る舞う理由
電流を流すループは磁場を生成します。この磁場には、右手の法則で定義される方向と強さがあります。ループの磁気モーメント($$\vec{m}$$)は次のように与えられます。
[\vec{m} = I \cdot A \cdot \hat{n}]
ただし:
- ($$I$$)は電流
- ($$A$$)はループの面積
- ($$\hat{n}$$)は面に垂直な単位ベクトル
| 要素 | 磁気モーメントへの影響 |
|---|---|
| 面積が大きい | 磁気モーメントが増加する |
| 電流が高い | 磁気モーメントが増加する |
| より多くのループ | 全体のモーメントを増幅させる |
私はエンジニアがカスタムコイルの磁気モーメントを計算するのを手伝ったことがあります。あるセンサークライアントのプロジェクトでは、ループ数を増やすことで、より弱い磁場を高精度で検出できるようになりました。
磁気モーメントのルールは何ですか?
磁気モーメントの方向を予測する方法はありますか?はい、簡単です。
右手の法則は磁気モーメントの方向を決定するために使われます:指を電流の方向に巻きつけ、親指がモーメントの方向を指します。

磁気モーメントの右手の法則–写真提供元 電気磁気学
実際のシステムへの法則の適用
コイルやループでは、磁気モーメントベクトルの方向は右手の法則に従います。これにより、次のことが助かります:
- 磁場センサーの設計
- 磁場中のコイルに働くトルクの理解
- 磁化された構造のN極・S極の判定
この法則が一般的な設定にどのように適用されるかは次の通りです:
| 設定 | 磁気モーメントの方向 |
|---|---|
| 水平時計回りのループ | ページ内に入る |
| 水平反時計回りのループ | ページから出る |
| 垂直コイル | 電流に基づいて上向きまたは下向き |
磁気アセンブリを設計するときは、常にコイルの向きをスケッチし、右手の法則を使用します。これにより時間を節約でき、誤りを避け、磁場が設計目標に沿っていることを保証します。
磁気モーメントはどう計算できますか?
磁気モーメントを推測する必要はありません—計算できます。
磁気モーメントは ( m = N \cdot I \cdot A ) を用いて計算されます。ここで N は巻数、I は電流、A は各ループの面積です。
例と応用例
式を分解しましょう:
[m = NIA]
- ( N ): コイルの巻数
- ( I ): コイルを流れる電流
- ( A ): 各ループに囲まれた面積(m²単位)
例:
コイルの巻数が100回、電流が0.5A、各ループの面積が0.01m²の場合:
[m = 100 \cdot 0.5 \cdot 0.01 = 0.5 \text{ A·m}^2]
実用例:
- 電動モーターのトルク計算
- 磁気センサーの磁場強度の推定
- インダクタやトランスの設計
| パラメータ | 単位 | 一般的な範囲 |
|---|---|---|
| ( I ) | アンペア | 0.01 – 10 A |
| ( A ) | 平方メートル | 0.0001 – 0.1 m² |
| ( m ) | A·m² | 0.001 – 10 A·m² |
顧客はしばしば、電流を増やさずに磁気効果を高める方法を尋ねます。答えは通常:ループ面積または巻き数を増やすことです。
結論
磁気モーメントは、磁気システムを理解するための重要な性質です。これは、磁石がどれだけ強く、どの方向に作用するかを示し、電子の微小なものから大きな発電機コイルまでを含みます。




[…] これら多様な応用例は、磁性材料の継続的な革新が、今日の日本市場における高性能と持続可能性の要求を満たすために不可欠である理由を示しています。基本的な磁気特性についてより深く理解するには、「磁気モーメントとは何か」をご覧ください。 […]